Look again at transformations in terms of vectors.
Scaling: x' = x * Sx, y' = y * Sy, which can be written as:
(x' y') = (x y) * (Sx 0)
(0 Sy)
Rotation: x' = x cos q - y sin q, y' = y cos q + x sin q, which can be written as:
(x' y') = (x y) * ( cos q sin q)
(-sin q cos q)
So if we wanted to scale and then rotate the object we could do the following:
(x' y') = (x y) * ( Sx 0 )
( 0 Sy )
(x" y") = (x' y') * ( cos q sin q )
(-sin q cos q)
But this is the same as:
(x" y") = (x y) * (Sx 0) * ( cos q sin q )
(0 Sy) (-sin q cos q )
= (x y) * ( Sx * cos q Sx * sin q)
(-Sy * sin q Sy * cos q )
Hence, we can concatenate the Scaling and Rotation matrices, and then multiply the old points by resultant matrix.
What about translation?
x' = x + Tx
y' = y + Ty
There isno way to express this as a multiplicative transformation with a 2D matrix. Therefore we go into hyperspace (N + 1 dimensions) , i.e., we embed 2D space into 3D space. We express all coordinates as (xh, yh, w) where w is the "z" coordinate. This is called a "Homogeneous" coordinate system.
The relationship between the original coordinates (x,y) and the homogeneous coordinates (xh, yh) is given by: xh = x * w, yh = y * w . We will generally use w = 1 so our 3D vector is (x, y, 1). Then we can express the modeling transformations as follows:
Translation (represented by T= (Tx,Ty)):
( 1 0 0 )
(x' y' 1) = (x y 1) * ( 0 1 0 )
( Tx Ty 1 )
which gives:
x' = x + 1 * Tx
y' = y + 1 * Ty
1 = 1
Scaling (represented by S= (Sx, Sy)):
( Sx 0 0 )
(x' y' 1) = (x y 1) * ( 0 Sy 0 )
( 0 0 1 )
which gives:
x' = x * Sx
y' = y * Sy
Rotation (represented by R(q):
( cos q sin q 0 )
(x' y' 1) = (x y 1) * (-sin q cos q 0 )
( 0 0 1 )
which gives: x' = x cos q - y sin q y' = y cos q + x sin q
So the solution to the problem of rotating or scaling an object about a point Po (xo, yo) is as follows:
1. Translate Po to origin: T(-xo, -yo)
2. Rotate: R(q)
3. Translate back to Po: T(+xo, +yo)
So (x' y') = (x y) * M with M = T(-xo , -yo) * R(q) * T(+xo , +yo )
Look at efficiency of constructing a composition matrix M and applying M to a set of points versus applying each transformation matrix to the set of points.
3D-matrix multiplication requires 3 * and 2 + for each element. Hence 3 x 9 = 27 (* & + operations) are required to multiply two 3D matrices, (Note: even with numeric data processors a * is about 1/3 the speed of a + so we are ignoring +) , So to concatenate N matrices requires: (N - 1)*( 27 ops.).
Multiplying a 3 element vector x 3D matrix 3 x 3 = 9 (ops.), But we have a special case since
( a d 0)
(x' y' 1) = (x y 1) * ( b e 0)
( c f 1)
which gives:
x' = ax + by + c 4 * and 4 + or 4 ops per point
y' = dx + ey + f
So if we applied each matrix individually to the points:
N = number of transformations = number of matrices
k = number of points
The total number of operation. = N * k * 4 (1)
For the case where we concatenate the transformations and then apply the resultant matrix tothe points:
(2) number of ops. = (N - 1) * 27 + 4 * k
At some value of k (1) > (2)
To find the crossover value of k, set the two equations equal to each other and find k:
27( N - 1 ) + 4k = 4Nk n > 2
27(N - 1) = 4Nk - 4k
27(N - 1) / 4(N - 1) = k = 27 / 4 or about 7 points.
Therefore, (2) is more efficient for any object with > 7 points.
Examples of transformations:
Look at scaling.
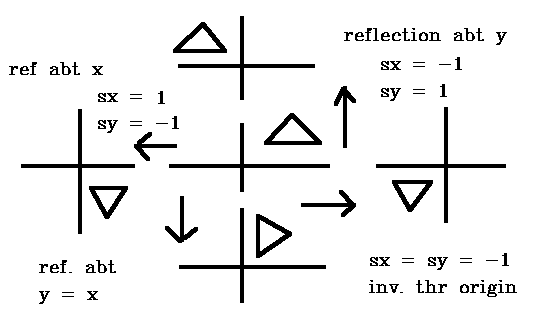
For bottom transformation this corresponds to :
1. R(-45) i.e. rotation by -45 (aligning y = x with x)
2. reflection about x-axis
3. R(+45 )
Composite matrix =
(0 1 0)
(1 0 0)
(0 1 0)
Main 2D Modeling page
HyperGraph Table of Contents.
HyperGraph Home page.