2D Window To Viewport Tranformation

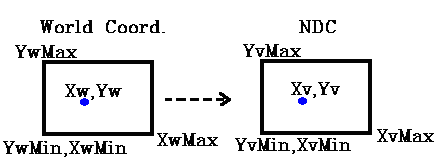
We want to map a point from WDC to Ndc, as shown below:

We can see from above that to maintain relative position we must have the following relationship:

Xw - Xwmin 		Xv - Xvmin
---------------- = ---------------------
Xwmax - Xwmin 		Xvmax - Xvmin 

Yw - Ywmin 		Yv - Yvmin
---------------- = ---------------------
Ywmax - Ywmin 		Yvmax - Yvmin 

We can rewrite above as

Xv = [(Xvmax - Xvmin)/(Xwmax - Xwmin)] * (Xw - Xwmin) + Xvmin
= Sx * (Xw - Xwmin) + Xvmin = Sx * Xw + Cx

where Sx = (Xvmax - Xvmin)/(Xwmax - Xwmin)
Cx = Sx * (- Xwmin) + Xvmin

Similarly for Y

Yv = [(Yvmax - Yvmin) / (Ywmax - Ywmin)] * (Yw - Ywmin) + Yvmin
= Sy * (Yw - Ywmin) + Yvmin = Sy * Yw + Cy

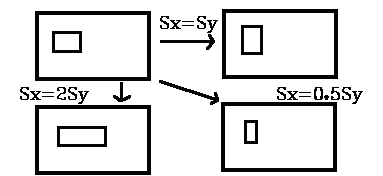
Note that Sx, Sy are "scaling" factors. If Sx = Sy the objects will retain same shape, else will be distorted, as shown in the example.

2D Viewing Transformation Main Page
HyperGraph Table of Contents.
HyperGraph Home page.